TRABAJO FINAL

Trabajo presentado por

-Valery Pardo

-Kenneth Araujo

-Breyner Callejas

-Hansel Viloria

1007

RADICACIÓN

La radicación es la operación inversa a la potenciación. Y consiste en que dados dos números, llamados radicando e índice, hallar un tercero, llamado raíz, tal que, elevado al índice, sea igual al radicando.

 

En la raíz cuadrada el índice es 2, aunque en este caso se omite. Consistiría en hallar un número conocido su cuadrado.

 

 

La raíz cuadrada de un número, a, es exacta cuando encontramos un número, b, que elevado al cuadrado es igual al radicando: b² = a.

 

Raíz cuadrada exacta

La raíz cuadrada exacta tiene de resto 0.

Radicando = (Raíz exacta)²

Cuadrados perfectos

Son los números que poseen raíces cuadradas exactas.

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, ...

Raíz cuadrada entera

Si un número no es cuadrado perfecto su raíz es entera.

Radicando = (Raíz entera)² + Resto

Algoritmo de la raíz cuadrada

1.Si el radicando tiene más de dos cifras, separamos las cifras en grupos de dos empezando por la derecha.

2.Calculamos la raíz cuadrada entera o exacta, del primer grupo de cifras por la izquierda.

¿Qué número elevado al cuadrado da 8?

8 no es un cuadrado perfecto, pero está comprendido entre dos cuadrados perfectos: 4 y 9, entonces tomaremos la raíz de la cuadrada del cuadrado perfecto por defecto: 2, y lo colocamos en la casilla correspondiente.

 

3.El cuadrado de la raíz obtenida se resta al primer grupo de cifras que aparecen en el radicando.

 

 El cuadrado de 2 es 4. se lo restamos a 8 y obtenemos 4.

4.Detrás del resto colocamos el siguiente grupo de cifras del radicando, separando del número formado la primera cifra a la derecha y dividiendo lo que resta por el duplo de la raíz anterior.

Bajamos 92, siendo la cantidad operable del radicando: 492.    

49 : 4 > 9, tomamos como resultado 9.

 

5. El cociente que se obtenga se coloca detrás del duplo de la raíz , multiplicando el número formado por él, y restándolo a la cantidad operable del radicando.

Si hubiésemos obtenido un valor superior a la a la cantidad operable del radicando, habríamos probado por 8, por 7...hasta encontrar un valor inferior.

6.El cociente obtenido es la segunda cifra de la raíz.

 

7. Bajamos el siguiente par de cifras y repetimos los pasos anteriores.

Como 5301 > 5125, probamos por 8.

Subimos el 8 a la raíz

 

8. Prueba de la raíz cuadrada.

Para que el resultado sea correcto, se tiene que cumplir:

Radicando= (Raíz entera)² + Resto

89 225= 298² + 421

 

 

TRIGONOMETRÍA

-¿Qué es la trigonometría?

La trigonometría es la subdivisión de las matemáticas que se encarga de calcular los elementos de los triángulos. Para esto se dedica a estudiar las relaciones entre los ángulos y los lados de los triángulos. La trigonometría realiza los cálculos de los elementos de un triángulo.

-¿Cuál es el origen de la trigonometría?

El origen de la trigonometría comienza con los babilonios y los egipcios. Estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, en los tiempos de la Grecia clásica, en el siglo II a. C.

-¿Quién fue el creador de la trigonometría?

Johann Müller

La trigonometría se introdujo en occidente sobre el siglo XII a través de traducciones de libros de astronomía arábigos. En Europa fue el matemático y astrónomo alemán Johann Müller, más conocido como Regiomontano, quien realizó el primer trabajo importante en esta materia, llamado “De Triangulus”.

 

 

 

 

 

-¿Cuál es la importancia de la trigonometría?

 

La trigonometría es fundamental en el estudio áreas de triángulos y otros polígonos regulares o no regulares, en el estudio de los volúmenes de poliedros, en múltiples cálculos a realizar en topografía, en mediciones de terreno u objetos, en dibujo técnico y en geometría descriptiva.

 

-¿Cuáles son las formulas de la trigonometría?

 

Éstas son:

·         Cosecante (csc): es la razón recíproca del seno. Es decir, csc α · sen α=1.

·         Secante (sec): la razón recíproca del coseno. Es decir, sec α · cos α=1.

·         Cotangente (cot): es la razón recíproca de la tangente. También en este caso, cot α · tan α=1.

 

 

 

 

 

-¿Cuáles son las 6 razones trigonométricas?

 

Se encuentran las seis razones trigonométricas (seno, coseno, tangente, secante, cosecante y cotangente) de un ángulo en un triángulo rectángulo dado.

 

-seno:

 

Cuando tenemos un triángulo rectángulo, el seno es igual a la longitud del lado opuesto al ángulo dividida por la longitud de la hipotenusa del triángulo.

 

 

 -coseno:

 

La ley de los cosenos establece: c ² = a ² + b ² – 2 ab cos C . Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras.

 

 

 

 

-tangente:

La tangente es igual a la longitud del lado opuesto al ángulo dividida por la longitud del lado adyacente. A pesar de que la tangente es definida con los ángulos de un triángulo rectángulo, la función tangente puede ser usada para cualquier ángulo.

 

 

-secante:

La secante es la razón trigonométrica recíproca del coseno. Es el recíproco o el inverso multiplicativo del coseno, es decir sec α · cos α=1. La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).

 

-cosecante:

La cosecante de un ángulo es igual a la longitud de la hipotenusa dividida por la longitud del lado opuesto al ángulo en el triángulo.

 

 

 

-cotangente:

La cotangente es la razón trigonométrica recíproca de la tangente. Es el recíproco o el inverso multiplicativo de la tangente, es decir tan α · cot α=1. La cotangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).

 

 

 

 

 

ÁNGULO

¿Qué es ángulo?

El ángulo es la porción del plano comprendida entre dos semirrectas (lados) con un origen común llamado vértice. Los ángulos parten de un punto y tienen dos líneas que salen desde ese punto y que generan una apertura representada por un arco. El grado de apertura de esos arcos (y no su extensión) está representado por el ángulo.

El concepto de ángulo corresponde a la geometría, una de las ramas de las matemáticas, pero también se aplica en otros campos como la ingeniería, la óptica o la astronomía.

La medición de los ángulos se realiza a partir del sistema sexagesimal que se expresa en grados (º), minutos (’) y segundos (’’). Un grado equivale a 60 minutos y un minuto equivale a 60 segundos. La cantidad de grados podrá ascender hasta 360, que es considerado el giro completo de una circunferencia. Por ejemplo: En el reloj de agujas, las agujas forman ángulos. A las 12 en punto, cuando las dos agujas apuntan para el mismo lado, el ángulo es de 0°; a las 3 de 90°; a las 6 de 180° y a las 9 de 270°.

Los ángulos están representados por una magnitud que puede ser analizada y comparada con otras, por lo que existen operaciones entre ángulos. Se puede sumar y restar ángulos entre sí o multiplicarlos y dividirlos por números enteros.

La recta que divide en dos partes iguales a un ángulo se llama bisectriz y cualquier punto de ella equidista de ambos lados del ángulo.

Tipos de ángulos

Un ángulo nulo es el que mide 0°.

Los ángulos se pueden clasificar de acuerdo a ciertos criterios.

Según su amplitud:

-          Ángulo nulo. Es el que mide 0°.

-          Ángulo agudo. Es el que mide entre 0° y 90°.

-          Ángulo recto. Es el que mide 90°.

-          Ángulo obtuso. Es el que mide entre 90° y 180°.

-          Ángulo llano. Es el que mide 180º.

-          Ángulo cóncavo. Es el que mide más de 180°.

-          Ángulo completo. Es el que mide 360°.

Según la relación con otro ángulo:

-          Ángulos suplementarios. Son ángulos que suman 180º.

-          Ángulos complementarios. Son ángulos que suman 90°.

Según su posición:

-          Ángulos consecutivos. Son ángulos que comparten un lado y el vértice.

-          Ángulos adyacentes. Son ángulos consecutivos y el lado que no comparten forma parte de la misma recta.

-          Ángulos opuestos por el vértice. Son ángulos que comparten el vértice pero ninguno de los lados.

Operaciones con ángulos

-          Sumas entre ángulos. Cuando se suman dos o más ángulos se deben sumar los grados (y también los minutos y los segundos si corresponde) de cada uno de los ángulos. Por ejemplo:
ángulo α + ángulo β = ángulo γ
90º      +      70º     = 160º

-          Restas entre ángulos. Cuando se restan dos o más ángulos se deben restar los grados (y también los minutos y los segundos si corresponde) de cada uno de los ángulos. Por ejemplo:
ángulo γ – ángulo β = ángulo α
160º     –     70º    = 90º

-          Multiplicaciones con ángulos. Cuando se multiplica un ángulo por un número natural se deben multiplicar los grados, los minutos y los segundos por ese número. En el caso de que los valores de los minutos o segundos supere los 60, se deberán pasar esas unidades a la siguiente escala. Por ejemplo:
ángulo α = 40º 10’ 20”
ángulo α x 2 = 40º x 2 + 10’ x 2 + 20” x 2 = 80º 20’ 40”

-          Divisiones con ángulos. Cuando se divide un ángulo por un número natural se deben dividir los grados, los minutos y los segundos por ese número. Al comenzar, se dividen los grados por el número y el resto que se obtiene se transforma en minutos (al multiplicarlo por 60) y se agrega a los minutos que ya se tenían. Se dividen los minutos y el resto se agrega a los segundos que ya se tenían que luego se dividen.

¿Cómo se mide un ángulo?

Para medir la amplitud de un ángulo, se necesita un instrumento de medición llamado transportador. El transportador está graduado, puede ser circular o semicircular y suele ser de plástico. Los pasos para medir un ángulo son:

1.     Se debe colocar el centro del transportador, que suele estar indicado con una ranura, en el vértice del ángulo (el origen del ángulo).

2.     Luego se debe corroborar que uno de los lados del ángulo coincida con la base del transportador.

3.     Se marca la graduación del lado restante en el transportador y esa es la amplitud del ángulo.

 

SISTEMA CIRCULAR O SISTEMA CÍCLICO

La unidad de medida de ángulos en el sistema cíclico es el radian, la medida del ángulo en el sistema cíclico, se determina a partir de la relación que existe entre el ángulo central de una circunferencia y arco obtenido por dicho ángulo.
Como la longitud de toda la circunferencia es 2πr, 360º equivalen a 2π radianes.  Por tanto, para pasar de grados sexagesimales a radianes, utilizamos la expresión 180º = π rad y realizamos regla de tres simple:

Ejemplo: Pasar 45º a radianes:

180º = π rad

45º =   x

 

ejemplos:

 

 

 

 

 

 

 

 en la siguiente figura se muestra alguno de las equivalencias entre algunas equivalencias en el sistema sexagesimal y el sistema cíclico.

 

 

 

 

 

 

convertir 135° a radianes

 

                       3

                      15

                      135 x π/180=3π/4

 

 

convertir 210° a radianes

 

 

7

35

105

210 x π/180=7π/6

 

 

 

 

 

¿Cuál es el instrumento que mide el sistema cíclico?

 

 

Según va recorriendo la circunferencia va describiendo un determinado ángulo. Para medir este y otros ángulos puedes utilizar como unidad el grado sexagesimal, que es la medida que resulta al dividir un giro completo en 360 partes iguales. ... Como la longitud de toda la circunferencia es 2πr, 360º equivalen a 2π.

 

ejemplo:

La ciclista está dando vueltas en un velódromo circular. Según va recorriendo la circunferencia va describiendo un determinado ángulo. 

Para medir este y otros ángulos puedes utilizar como unidad el grado sexagesimal, que es la medida que resulta al dividir un ángulo recto en 90 partes iguales. 

Por tanto, la circunferencia completa mide 360º sexagesimales. 


Pero en trigonometría vas a necesitar otra unidad para medir ángulos, el radián.

Como la longitud de toda la circunferencia es 2πr, 360º equivalen a 2π radianes. 
Por tanto, para pasar de grados sexagesimales a radianes, obtenemos la expresión:

Y para pasar de radianes a grados sexagesimales, tenemos:

 

TEOREMA DE PITÁGORAS

El teorema de Pitágoras es la relación que existe entre los lados de un triángulo rectángulo. Este establece que el área de un cuadrado con el lado más largo del triángulo rectángulo es igual a la suma de las áreas de los cuadrados formados con los otros dos lados del triángulo.

Un triángulo rectángulo es aquel polígono de tres lados que tiene un ángulo de 90º, también conocido como ángulo recto. Los catetos son los lados que forman el ángulo recto y la hipotenusa es el lado más largo del triángulo frente al ángulo recto.

A partir de la longitud de los catetos y la hipotenusa, el teorema de Pitágoras se expresa como la suma de los catetos al cuadrado es igual a la hipotenusa al cuadrado.

Fórmula del teorema de Pitágoras

El teorema de Pitágoras establece que la suma de los catetos al cuadrado es igual al cuadrado de la hipotenusa.

El teorema de Pitágoras se expresa de forma algebraica por la ecuación:

donde a y b son los catetos del triángulo y c es la hipotenusa. Cuando conocemos los valores de los catetos, podemos calcular la longitud de la hipotenusa por la fórmula:

Si conocemos el valor de la hipotenusa y de uno de los catetos, podemos calcular el otro cateto con la siguiente fórmula:

Ejemplos de teorema de Pitágoras

Una de los ejemplos del teorema de Pitágoras es el cálculo de distancias entre dos puntos, siempre y cuando exista un triángulo rectángulo en sus límites.

Por ejemplo, tenemos una pared de 2,70 metros de alto y queremos poner una escalera con una separación de 70 cm. Podemos calcular la longitud de la escalera de la siguiente manera:

• Se establece un ángulo recto entre la pared y el piso;
• La altura de la pared (2,7 m) y la separación entre la pared y la escalera a nivel del piso (70 cm) son los catetos; y
• La escalera representa la hipotenusa.

·         Usamos la fórmula:

·        

·         donde c es la hipotenusa (la medida de la escalera), a y b son los catetos:

·        

·         Así, la escalera debe ser de al menos 279 cm para llegar al tope de la pared.

·         Instalando la TV

·         El tamaño de los aparatos de TV se expresa como la diagonal de la pantalla, es decir, la distancia desde la esquina izquierda arriba hasta la esquina derecha abajo.

·         Así, una televisión de 50 pulgadas tiene una diagonal de 127 cm, porque una pulgada es igual a 2.54 cm (50x2.54=127).

·         Si sabemos la altura, podemos calcular el ancho del aparato:

·        

·         Aplicaciones del teorema de Pitágoras

·         Física

·         En física es clave el uso del teorema de Pitágoras en diferentes cálculos. Por ejemplo, si se quiere calcular la velocidad relativa a la tierra de un avión que vuela hacia el norte con una velocidad de 240 km/h pero con un viento que sopla a 100 km/h hacia el este.

·         Arquitectura y construcción

·         En arquitectura, carpintería y otras áreas de la construcción, el teorema de Pitágoras es ampliamente utilizado. Por ejemplo, si se conoce la altura de un techo y la distancia que tiene que cubrir, se usa el teorema de Pitágoras para cortar las vigas diagonales.

·         También se usa para asegurar que en las construcciones se forman ángulos rectos en las esquinas. Al medir los lados del triángulo, si estos coinciden con el teorema de Pitágoras, tendremos la seguridad que hay un ángulo recto.

Navegación

Los marineros usan el teorema de Pitágoras para buscar la distancia más corta entre dos lugares cuando navegan.

Por ejemplo, si se tiene que ir un punto que está a 3000 metros al norte y 5000 metros al este, la distancia más corta será la hipotenusa:

 

 

 

RAZONES TRIGONOMÉTRICAS DE UN TRIÁNGULO RECTÁNGULO

 

La trigonometría, enfocada en sus inicios solo al estudio de los triángulos, se utilizó durante siglos en topografía, navegación y astronomía.

Etimológicamente, trigon significa triángulo, y metron, medida. Por lo tanto, trigonometría se puede definir como "medida de triángulos".

Para establecer las razones trigonométricas, en cualquier triángulo rectángulo, es necesario conocer sus elementos. Para ello, veamos la figura a la derecha:

Los ángulos con vértice en A y C son agudos, el ángulo con vértice en B es recto.

Este triángulo se caracteriza por que los lados de los ángulos agudos (α y γ) son la hipotenusa y un cateto, y los lados del ángulo recto (β) son los catetos.

Cada uno de los ángulos agudos del triángulo, uno de cuyos lados es la hipotenusa, se relaciona con los catetos, que pueden ser cateto opuesto al ángulo o cateto adyacente al ángulo.

Cateto adyacente es aquel que forma parte del ángulo al cual se hace referencia.

Cateto opuesto es el lado que no forma parte del ángulo que se toma como referencia y se encuentra enfrente de este.

Con los siguientes ejemplos, veamos lo dicho:

Si consideramos el ángulo α	Si consideramos el ángulo γ
cateto adyacente cateto opuesto	cateto adyacente  cateto opuesto

Por convención, como vemos en los ejemplos, los trazos que son lados del triángulo se pueden representar con las letras mayúsculas correspondientes a sus dos extremos, coronadas con una línea; o bien, con una letra minúscula enfrentando a la correspondiente mayúscula de los ángulos.

Aprendido y recordado lo anterior, veremos ahora que las razones o relaciones trigonométricas se establecen entre dos lados de un triángulo rectángulo en relación con cada uno de sus ángulos agudos. También se llaman Funciones trigonométricas.

Seis son las razones o funciones trigonométricas que se pueden establecer para cualquiera de los dos ángulos agudos en un triángulo rectángulo; de ellas, tres son fundamentales y tres son recíprocas, como lo vemos en el siguiente cuadro:

Funciones (razones) trigonométricas
Fundamentales		Recíprocas
sen	seno	cosec (csc)	cosecante
cos	coseno	sec	secante
tan (tg)	tangente	cotan (cotg)	cotangente

Veamos un ejemplo, para un ángulo α:

Sea el ángulo BACde medida α (siempre menor de 90º) en el triángulo rectángulo ABC. Los lados BC y BA son los catetos y AC, la hipotenusa.

 

En este triángulo rectángulo, las razones trigonométricas con respecto a alfa (α) se definen como:

Seno

Seno, es la razón (división) entre el cateto opuesto al ángulo y la hipotenusa

Coseno

coseno, es la razón (división) entre el cateto adyacente al ángulo y la hipotenusa

Tangente

tangente, es la razón entre el cateto opuesto al ángulo y el cateto adyacente al mismo.

Estas tres (seno, coseno, tangente) son las razones fundamentales que se pueden establecer entre un ángulo agudo y los lados del triángulo rectángulo del cual forman parte.

A cada razón fundamental corresponde una razón recíproca, llamadas así por que cada una es la inversa de otra fundamental.

Las tres siguientes son las razones recíprocas que se pueden establecer respecto al mismo ángulo:

Cosecante

cosecante, es la razón entre la hipotenusa y el cateto opuesto al ángulo, y como es la recíproca del seno de α se puede expresar como

Secante

secante, es la razón entre la hipotenusa y el cateto adyacente al ángulo, y como es la reciproca del coseno de α se puede expresar como

Cotangente

cotangente, es la razón entre el cateto adyacente al ángulo y el cateto puesto al mismo, y como es la recíproca de la tangente de α se puede expresar como

 

Ahora, hagamos un ejercicio:

dado el triángulo ABC rectángulo en B (figura a la derecha).

Sean sus catetos AB = 8 cm y BC = 6 cm.

Aplicamos el Teorema de Pitágoras y calculamos la hipotenusa, que es:

82 + 62 = 102; o sea, es igual a 10 cm

entonces podemos calcular las razones trigonométricas:

 

 

 

ÁNGULOS NOTABLES

 

Los ángulos notables son aquellos que aparecen frecuentemente en la resolución de problemas. Estos ángulos son los que miden:
30°, 45° y 60°. Para calcular los valores de las funciones trigonométricas vamos a dibujar triángulos rectángulos que tengan a estos ángulos en uno de sus ángulos internos. Para esto, utilizamos la figura utilizada en secciones previas:

Dado que el triángulo es rectángulo, y uno de los ángulos agudos mide 30°, el otro debe medir 60°. Con eso, podemos calcular los valores de las funciones trigonométricas de estos ángulos. Ya calculamos los valores para 30°. Ahora calculamos los valores para 60° modificando la figura como se muestra enseguida:

Observa que la altura del cuadrado mide 2 √3, porque al aplicar el teorema de Pitágoras:

 

Los valores de las funciones trigonométricas para 
son:

  

Para calcular los valores correspondientes al ángulo de , vamos a trazar un cuadrilátero regular (un cuadrado) y vamos a considerar una de sus diagonales:

Para calcular la longitud de la diagonal del cuadrado utilizamos el teorema de Pitágoras:

  

Consideramos solamente el triángulo que se forma con dos de los lados
del cuadrado y su diagonal que corresponde a la hipotenusa del
triángulo rectángulo:

Con los valores obtenidos podemos crear la siguiente tabla de resumen
de los valores de las funciones trigonométricas de los ángulos notables:

%

 

Estos valores nos serán de gran utilidad para resolver problemas en lo sucesivo.

 

RAZONES TRIGONOMETRICAS DE LOS ÁNGULOS NOTABLES

Llamamos ángulos notables a los ángulos de 30⁰,45⁰ y 60⁰, o en su equivalente en radianes 
 

, respectivamente.

 Para obtener los valores exactos de las funciones trigonométricas de estos ángulos, se adoptan 2 triángulos que por conveniencia y facilidad tiene las siguientes dimensiones.

 1) Para funciones de 45⁰, se considera un triángulo rectángulo Isósceles, cuyos catetos convenientemente miden 1, así:

 NOTA: La hipotenusa se obtiene aplicando teorema de Pitágoras.

-Calculando funciones trigonométricas para un ángulo de 45⁰.

2) Para calcular los valores de las funciones de 30⁰ y 60⁰, se considera un triángulo equilátero de lado 2 y se procede como sigue:

Se traza una altura (Línea punteada), la cual por la simetría del triángulo equilátero es una bisectriz, es decir parte a la mitad el ángulo de 60⁰ y además intercepta con la mitad de la base.

 Por Pitágoras se determina que el valor de la altura (línea punteada) es:

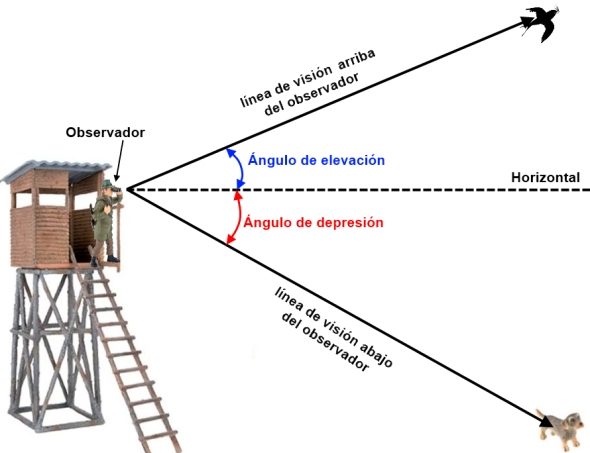
ÁNGULOS DE ELEVACIÓN Y DEPRESIÓN

Llamamos ángulo de elevación al que forman la horizontal del observador y el lugar observado cuando este está situado arriba del observador y ángulo de depresión al que se va a medir por debajo de la horizontal.

 

Teorema del seno

Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.

Aplicaciones

Este teorema es útil para resolver problemas si los datos dados entran en alguno de los siguientes casos:

1 Si tenemos las medidas de 2 lados de un triángulo, y el ángulo opuesto a uno de ellos.

Aplicando el teorema inmediatamente puedo obtener el ángulo opuesto al otro lado que conocemos

2 Si tenemos las medidas de 2 ángulos de un triángulo, y el lado opuesto a uno de ellos.

Aplicando el teorema inmediatamente puedo obtener el lado opuesto al otro ángulo que conocemos.

3 También se puede aplicar cuando se conocen 2 ángulos del triángulo y un lado que no es opuesto a ninguno de ellos, sólo que requiere un paso extra, que es obtener el otro ángulo del triángulo.

Esto es posible porque sabemos que la suma de los ángulos de un triángulo es 180°.
Por ejemplo, en la imagen de arriba, el ángulo B se obtiene de restar los otros 2 ángulos a 180:

Ignorando uno de los ángulos dados originalmente, ya tenemos los datos de 2 ángulos y el lado opuesto de uno de ellos, como el segundo caso mencionado en las aplicaciones.

Teorema del coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Aplicaciones

Este teorema es útil para resolver problemas,

1 Si tenemos la medida de un ángulo y de los lados adyacentes a este.

Aplicando el teorema podemos obtener el tercer lado, es decir el lado opuesto al ángulo que tenemos, pues

2 Si tenemos la medida de los 3 lados de un triángulo

Aplicando el teorema podemos obtener cualquier ángulo, pues